S4.交叉结构-自动特征工程

介绍运用于推荐系统的交叉结构
搜广推
王树森
Author

Hahabula

Published

2025-04-16

Modified

2025-04-23

该篇文章介绍的交叉结构均可以用于各种神经网络中。

个人感受

感觉这个部分还是某种特征工程只是这种特征工程是自动实现的。

1 Factorization Machines(FM)——因子分解机

因子分解机是一种用于处理高维稀疏数据的预测模型，特别适用于推荐系统、点击率预测等场景。它通过分解特征的交互作用来捕捉复杂的非线性关系，同时保持了线性模型的可解释性。因子分解机的核心思想是将特征之间的交互表示为低维因子向量的内积。

1.1 线性模型

有d个特征，记作\(x = [x_1, x_2, \cdots, x_d]\)，线性模型的预测函数为：

\[ \hat{y} = w_0 + \sum_{i=1}^d w_ix_i \]

该模型存在 \(n+1\) 个参数：\(w_0\) 和 \(w_1, w_2, \cdots, w_d\)。

预测是特征的加权和（只加不乘，未涉及特征交叉）

1.2 二阶交叉特征

1.2.1 模型

二阶交叉特征的模型是：

\[ \hat{y} = w_0 + \sum_{i=1}^d w_ix_i + \sum_{i=1}^d\sum_{j=i+1}^d u_{ij} x_ix_j \tag{1}\]

1.2.2 FM

Equation 1 模型有 \(O(d^2)\)，一旦自变量过多将会导致模型参数量巨大，容易出现过拟合的现象。

如何减少参数量？

考虑 \(U={u_{ij}}\) 是对称矩阵，即 \(u_{ij}=u_{ji}\)，那么便可进行矩阵的特征值分解：

仅考虑前 \(k\) 个特征向量，实现对参数矩阵的降维，即FM模型的表达式如下：

\[ \hat{y} = w_0 + \sum_{i=1}^k w_ix_i + \sum_{i=1}^k\sum_{j=i+1}^k \langle v_i, v_j \rangle x_ix_j \]

其中，\(\langle v_i, v_j \rangle\) 是 \(v_i\) 和 \(v_j\) 的内积，\(v_i\) 是第 \(i\) 个特征向量。

注意

⚠️ FM在业界基本过时，但是它的思想是具有启发的，值得学习。

2 深度交叉网络（DCN）

深度交叉网络是一种结合交叉层和深度神经网络来捕捉特征高阶交互信息的模型，广泛应用于推荐系统和点击率预测等领域。

2.1 交叉层

其数学表达式如下：

\[ x_{i+1}=x_0\oplus(W\cdot x_i+b)+x_i \]

该交叉层中采用了残差连接(resnet)见 残差连接

2.2 交叉网络

交叉网络的优势

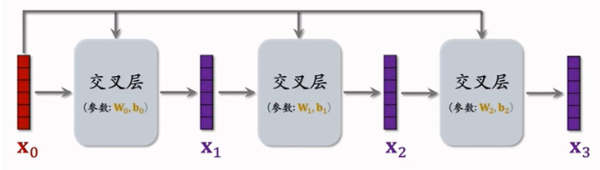
交叉网络更直接地捕捉特征之间的交互关系，计算复杂度较小/可解释性较强。

2.3 深度交叉网络结构

  1. 与DNN合作，交叉网络负责显示地构建高阶特征交互。
  2. DNN捕捉非线性特征和复杂模式。

2.4 tensorflow的实现

# TensorFlow实现交叉网络(DCN)
import tensorflow as tf
from tensorflow.keras import layers, Model

class CrossLayer(layers.Layer):
    """交叉层实现"""
    def __init__(self, units, **kwargs):
        super(CrossLayer, self).__init__(**kwargs)
        self.units = units
        
    def build(self, input_shape):
        # 创建权重矩阵W和偏置b
        self.w = self.add_weight(
            shape=(input_shape[-1], self.units),
            initializer='glorot_uniform',
            trainable=True,
            name='cross_weight'
        )
        self.b = self.add_weight(
            shape=(self.units,),
            initializer='zeros',
            trainable=True,
            name='cross_bias'
        )
        super(CrossLayer, self).build(input_shape)
        
    def call(self, inputs, x0=None):
        if x0 is None:
            x0 = inputs
        # 实现交叉层的计算: x_{i+1} = x_0 ⊙ (W·x_i + b) + x_i
        # 其中⊙表示元素级别的乘法
        x = tf.matmul(inputs, self.w) + self.b  # W·x_i + b
        x = tf.multiply(x0, x)  # x_0 ⊙ (W·x_i + b)
        x = x + inputs  # 加上残差连接
        return x

class DeepCrossNetwork(Model):
    """深度交叉网络(DCN)实现"""
    def __init__(self, cross_layers=3, dnn_hidden_units=[128, 64], num_classes=1, **kwargs):
        super(DeepCrossNetwork, self).__init__(**kwargs)
        self.cross_layers_num = cross_layers
        self.dnn_hidden_units = dnn_hidden_units
        self.num_classes = num_classes
        
        # 交叉网络部分
        self.cross_layers = []
        for i in range(self.cross_layers_num):
            self.cross_layers.append(CrossLayer(units=1, name=f'cross_layer_{i}'))
        
        # 深度网络部分
        self.dnn_layers = []
        for i, units in enumerate(self.dnn_hidden_units):
            self.dnn_layers.append(layers.Dense(
                units, activation='relu', name=f'dnn_layer_{i}'
            ))
        
        # 合并层
        self.combine = layers.Concatenate(axis=1)
        
        # 输出层
        self.output_layer = layers.Dense(
            self.num_classes, activation='sigmoid' if self.num_classes == 1 else 'softmax'
        )
        
    def call(self, inputs):
        # 交叉网络部分
        cross_output = inputs
        x0 = inputs
        for cross_layer in self.cross_layers:
            cross_output = cross_layer(cross_output, x0)
        
        # 深度网络部分
        dnn_output = inputs
        for dnn_layer in self.dnn_layers:
            dnn_output = dnn_layer(dnn_output)
        
        # 合并交叉网络和深度网络的输出
        combined = self.combine([cross_output, dnn_output])
        
        # 输出层
        output = self.output_layer(combined)
        
        return output

# 使用示例
def build_dcn_model(feature_dim=10):
    """构建DCN模型"""
    inputs = layers.Input(shape=(feature_dim,))
    model = DeepCrossNetwork(
        cross_layers=3,
        dnn_hidden_units=[128, 64],
        num_classes=1
    )
    outputs = model(inputs)
    model = Model(inputs=inputs, outputs=outputs)
    model.compile(
        optimizer='adam',
        loss='binary_crossentropy',
        metrics=['accuracy']
    )
    return model

# 创建并查看模型
model = build_dcn_model(feature_dim=10)
model.summary()
Model: "model"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 input_1 (InputLayer)        [(None, 10)]              0         
                                                                 
 deep_cross_network (DeepCro  (None, 1)                9772      
 ssNetwork)                                                      
                                                                 
=================================================================
Total params: 9,772
Trainable params: 9,772
Non-trainable params: 0
_________________________________________________________________
适用范围

之前用于召回、排序的模型，如双塔模型、多目标排序模型、MMoEd模型等的神经网络部分，都可以用这种深度交叉网络。

劣势
  • 受交叉层数限制，只能不做有限阶的特征交互。
  • 要求输入的数据得具有一定的稀疏性
  • 参数的效率低

3 LHUC网络

LHUC(Learned Hidden Unit Contribution) 起源于语音识别，后来快手将LHUC应用于精排，称作PPNet。

3.1 语音识别中的应用

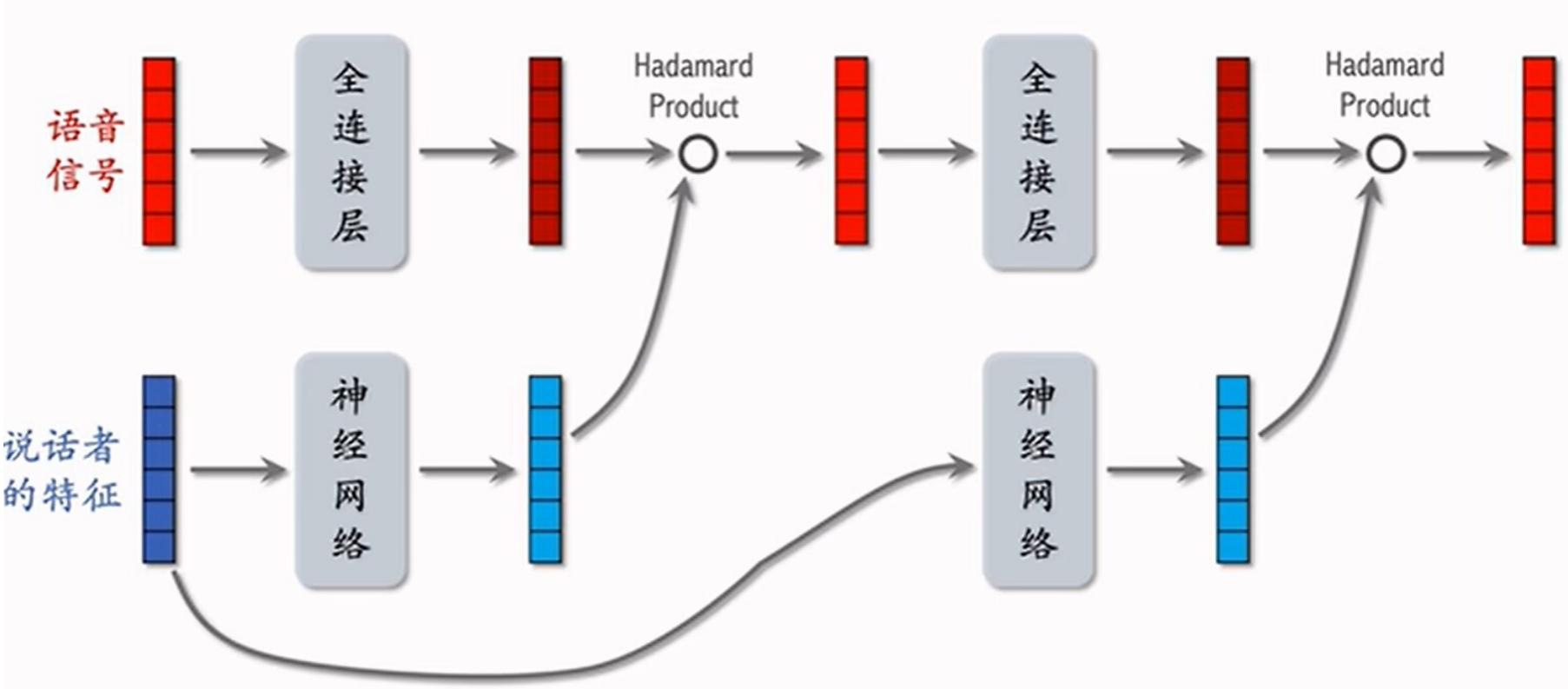
LHUC⽹络结构实现了语⾳信号与说话者特征的融合，说话者特征经过的神经⽹络通常是全连接层+sigmoid函数值x2，这样的处理可以用于放大某些特征，缩小某些特征。

3.2 推荐系统中的应用

  • 语音信号 ➡️ 物品特征
  • 说话者特征 ➡️ 用户特征

4 SENet

SENet（Squeeze-and-Excitation Network）是一种深度学习网络结构，通过引入通道注意力机制来增强网络对不同特征通道的区分能力。具体来说，SENet会在每个残差块中添加两个新的层：首先通过全局平均池化层“压缩”（squeeze）特征图，然后通过全连接层和激活函数“激励”（excite）特征通道的权重，从而使得网络能够自适应地调整各个通道的重要性，提升模型的表现力和泛化能力。

4.1 SENet的架构

先对特征进⾏embedding得到m×k的向量结构，m⾏代表有m个特征（⽤⼾ID、物品ID、用户或者物品特征），m个向量的作⽤就是做特征的field-wise加权（如果学出某个特点对任务的重要性不⾼，就对这个特点降权）

field-wise

例如，⽤⼾ID embedding是64维向量，那么这64个元素算1个field，获得相同权重如果有m个fields，那么权重向量就是m维重要的field权重⾼，不重要的field权重低实际上，Embedding向量维度可以不同。

5 Bilinear Cross

Bilinear Cross是一种交叉网络结构，用于捕捉输入特征之间的二阶交互信息。它通过双线性形式的参数矩阵来学习特征之间的组合效应，从而能够更好地建模复杂的数据关系，常用于推荐系统、点击率预测等场景，以提高模型的表达能力和预测性能。

5.1 field间特征交叉

内积

内积

哈达玛积

哈达玛积
  1. 内积

\[ x_i \cdot x_j = \sum_{k=1}^d x_{ik} x_{jk} \]

m个fields会有 \(m^2\) 个实数

  1. 哈达玛积

\[ (x_i \odot x_j)_k = x_{ik} x_{jk}, \quad k=1,2, \cdots, d \]

m个fields会有 \(m^2\) 个向量

5.2 Bilinear Cross的模型

  1. 内积型

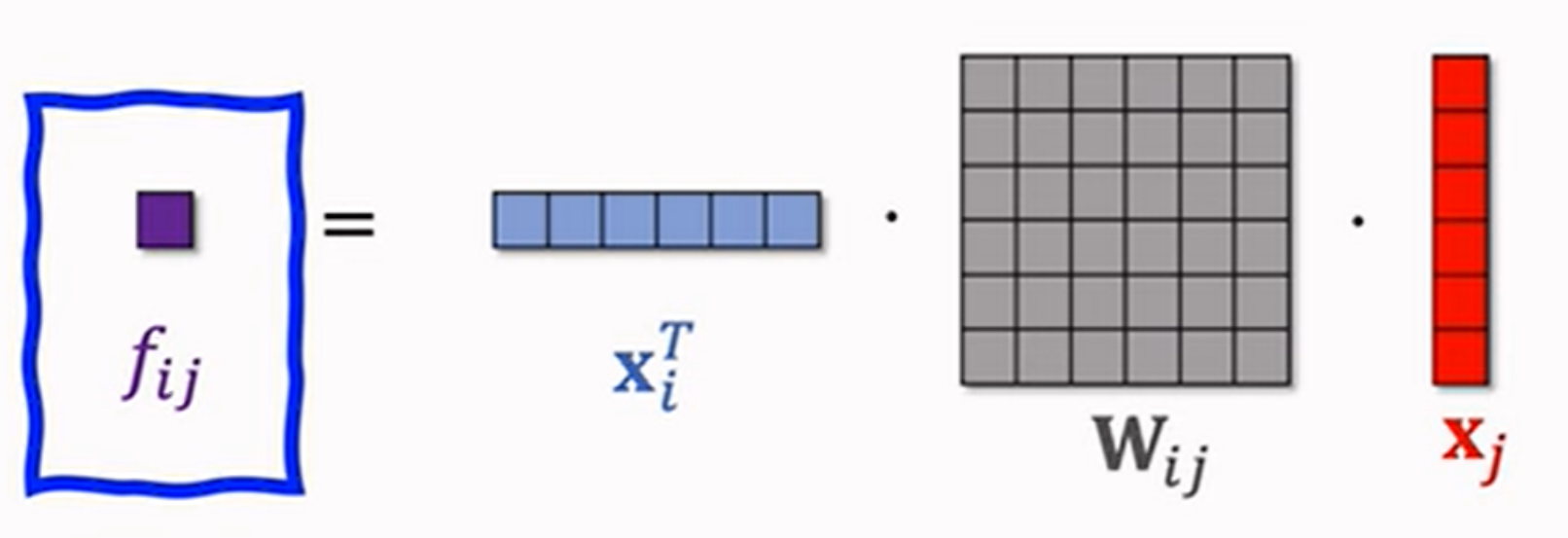
如果有m个fields，那么就有 \(C_m^2\approx \frac{m^2}{2}\) 个参数矩阵，会导致参数数量极⼤，因此需要让重要的特征进⾏交叉，⽽不能所有特征都进⾏交叉。

参数矩阵个数

两个field不同顺序的交叉无需两个参数矩阵，只需要将另一个参数矩阵进行转置即可。

  1. 哈达玛积型

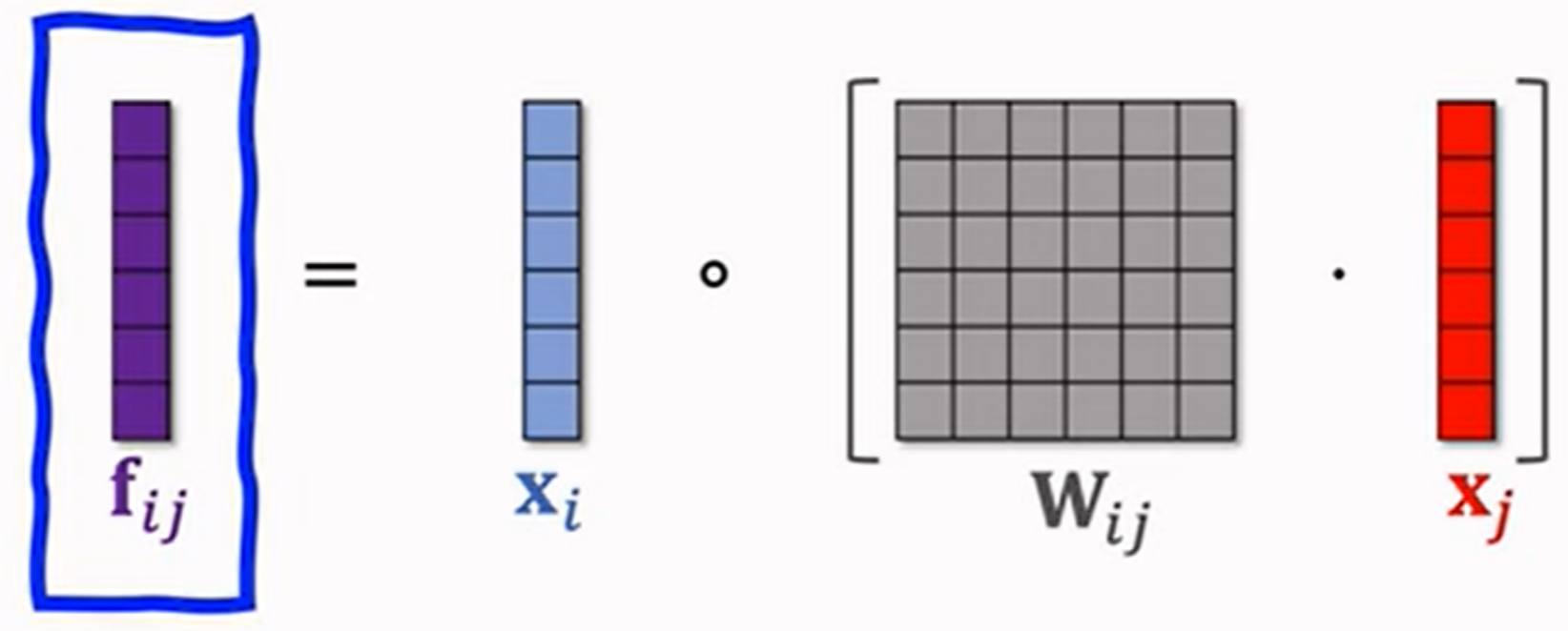
得到 \(m^2\) 个向量，容量太⼤了，⽽且很多都是⽆意义的特征，实际⼯程中需要指定⼀些特征做交叉。

6 FiBiNet

FiBiNet（Feature Interaction Bilinear Network）是一种深度学习网络结构，通过引入特征交互的双线性形式的参数矩阵来学习特征之间的组合效应，从而能够更好地建模复杂的数据关系，常用于推荐系统、点击率预测等场景，以提高模型的表达能力和预测性能。

该深度学习网络是将 SENet 和 Bilinear Cross 进⾏结合。

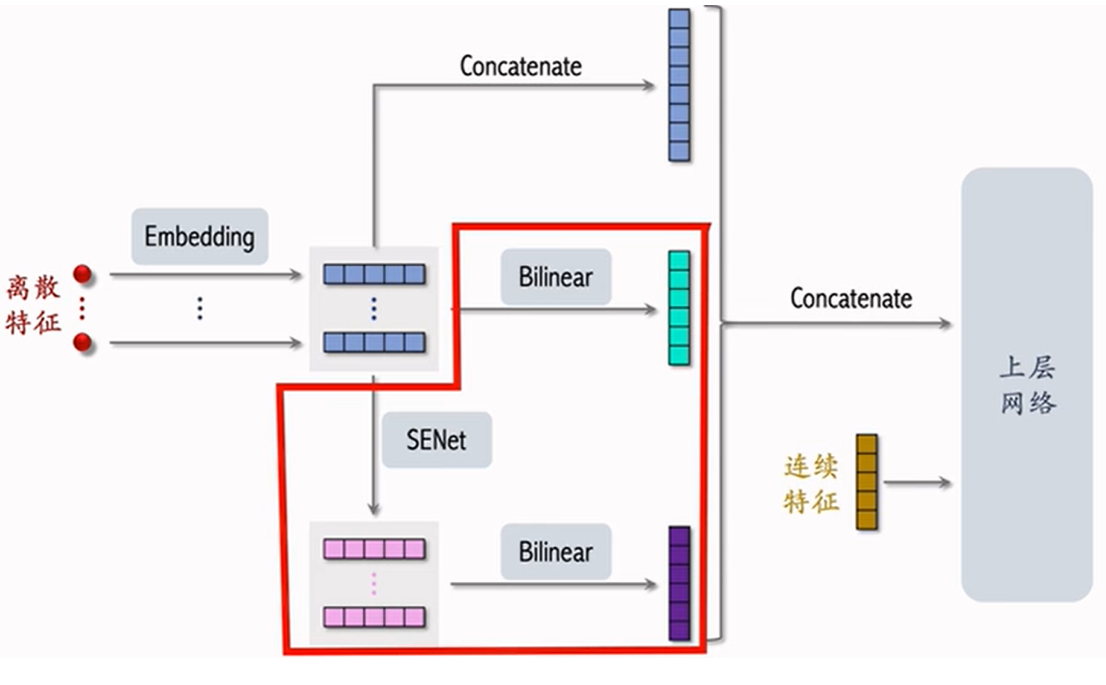
相⽐起多⽬标排序模型来说，FiBiNet多了红⾊圈出来的部分，对特征的embedding ⼀路进⾏SENet加权再bilinear交叉，另⼀路直接进⾏bilinear交叉，最后与 embedding直接的串接再三路合并，和连续特征⼀起输⼊上层⽹络

Back to top